Data Structures
While the greater part of Arduino programming is about responding to events and monitoring responses, a well-versed Arduino C programmer will be faced by the need to manage chunks of data. Managing data with restricted data memory space is always going to be a challenge. If we add to that challenge the frequent need to handle incoming data collected at quite a pace we have some interesting programming techniques to explore.
In this chapter, I want to take a look at some modest data compression techniques including constructing and navigating a binary tree and also a FIFO (first in first out) buffer. It may sound like we are entering the field of computer science but these are practical tools that can be applied in many projects. Of course, we need to start with a problem domain and I have picked one that should be easily understood and yet expose a nice set of technical requirements.
This chapter is going to start by tackling the rather historical subject of Morse code. Samuel Morse invented the code named after him alongside the telegraph and they were both first publicly demonstrated in 1844. While the telegraph (and the telegraph code) solved the communications problem of an earlier era you might be wondering how that is worth exploring in an age where our devices can plug into Wi-Fi, Bluetooth and other radio data formats. I would suggest that all forms of signalled communication face the same issues and that Morse code has the benefit of being “human sensible”. With a little effort, it is perfectly possible to become proficient in encoding and decoding Morse and thus we have an additional angle when it comes to debugging. Not that it will be necessary to become skilled in Morse to benefit from the insights it can give when it comes to data handling.
First – just what is Morse code? Morse code is a method for transmitting text as a series of pulses that might be received as sound, light, voltage changes or radio waves. Individual letters and numbers are encoded as a sequence of dots and dashes. A dash is transmitted as a pulse that is three times the length of a dot. Each dot or dash is separated by an interval that is equal to the length of a dot. Individual letters are separated by an interval equal to a dash and words are separated by an interval equal to two dashes. You might then ask, just how long is a dot? The slightly disconcerting answer is that it depends upon the transmission rate and will vary, especially between human operators. A skilled human can work at speeds in excess of 40 words a minute but you can get a scout’s badge at just 5 words a minute. For human sources, the code element lengths are all relative but we can perhaps tie them down a bit for a micro-processor based source.
I rather like the idea of having two or more micro-robots communicating using Morse to pass information about ambient conditions or discoveries. Having them communicate using Morse would enable me to “listen in” as well as observe.
International Morse Code
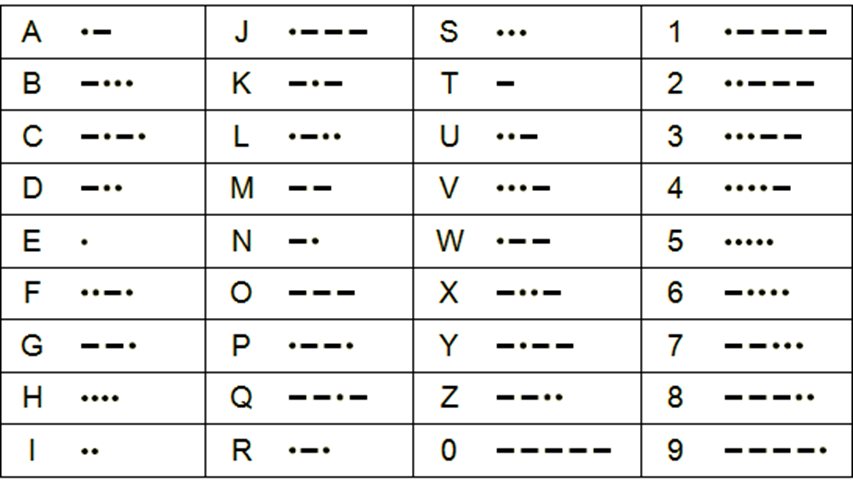
There are additional codes recognised but I am going to stick with the original list. You might notice that the length of the code for any given letter is in proportion to the frequency of its use in English. The most common English letter is E and this is represented by a single dot. The letter T is the next most common and this is encoded as a single dash. The least common letters make use of 4 dots and dashes and finally the numerals 0 to 9 are encoded as 5 dots and/or dashes.
If we wanted to write a function to encode and transmit some text as Morse code then we would need a look-up table of some sort to obtain the code for any given character. We might try an array of pointers to char arrays representing each individual character’s code. This could be created with:
const char* mCodes[] = {
".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..",
".---", "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.",
"...", "-", "..-", "...-", ".--", "-..-", "-.--", "--..", "-----",
".----", "..---", "...--", "....-", ".....", "-....", "--...",
"---..", "----."
};
We are already applying some programming technique here as this storage model does not need to store the character represented by the individual codes. We can use the array position to manage that. The first 26 codes represent the letters A through Z while the next 10 codes are the numbers 0 to 9. That is an immediate memory saving. However, with the shortest char array (Morse code for E or T) being 2 bytes long and the numeric characters needing 6 bytes for storage that is going to use up some 312 bytes of precious memory. We could move those bytes into PROGMEM or the EPROM but the issue still holds. Any communications function is only going to represent a small part of the overall code base so we need to minimise the data storage requirement.
Pondering this while taking some exercise, I came up with a wizard scheme for encoding the Morse code elements in just 36 bytes. A later reality check via the Internet found that my idea had been thought of before but that is validation and validation is always good. My idea was that we could encode the dots and dashes as binary digits (perhaps 1 for a Dash and a 0 for a dot) in a byte. However, that did not solve the problem of the variable length of different coded characters. We would need a way to distinguish between bits that represented a dot and unused bits. Then I realised that with a minimum of 3 bits left over in each byte we could also encode the number of bits in a given byte actually used to represent a specific character code.
The array mCode[] below stores the Morse code dots and dashes in the high order bits and the number of code elements for a given character in the lowest 3 bits.
byte mCode[] = {
B01000010, B10000100, B10100100, B10000011, B00000001, B00100100,
B11000011, B00000100, B00000010, B01110100, B10100011, B01000100,
B11000010, B10000010, B11100011, B01100100, B11010100, B01000011,
B00000011, B10000001, B00100011, B00010100, B01100011, B10010100,
B10110100, B11000100, B11111101, B01111101, B00111101, B00011101,
B00001101, B00000101, B10000101, B11000101, B11100101, B11110101
};
The first byte array element represents “A” which is dot dash so the first high order bits are 01 and the number of bits is represented by setting the bit count to 010 (binary for decimal 2) in the low order bits.
The byte array is a little more than 11% of the original look-up table which is a nice data compression. Further inspection of the codes would indicate that it would be possible to reduce the byte storage by a further 10 bytes as the numeric digits are encoded in a very regular pattern that could be returned by a short function.
The additional Morse code punctuation characters are encoded using 6 dashes and dots. If these symbols were required then they could be stored in a separate array with the code length omitted as it would always be the same constant value.
You might worry that it is complex and process intensive to extract the code from the byte encoding. Well we can check the process by an exercise to convert the byte encoding to a char array to make a comparison to the values in our first Morse storage array (mCodes[]). This was exactly the cross check I used to ensure that the byte values were correctly entered to my program.
Include the mCodes[] and mCode[] arrays from above into a new program. It is worth making the effort with the mCode[] array in particular as that is going to be copied and pasted into more programs as we progress through this chapter.
#define HIBIT_MASK B10000000
void setup() {
Serial.begin(115200);
int x;
byte bc;
char code[6];
for (int i = 0; i < 36; i++) {
Serial.print(mCodes[i]);
Serial.print(" : ");
bc = mCode[i]; // copy the byte to manipulate it
x = bc & ((1 << 3)-1); // set x to value of the lower 3 bits
memset(&code[0], 0, 6); // clear out target char array
for(int j = 0; j < x; j++){
if((bc & HIBIT_MASK) == 0) // take care with the brackets
{
code[j] = '.';
} else {
code[j] = '-';
}
bc = bc << 1; // shift the code bits left
}
Serial.println(code); // ready for visual comparison
}
}
Some of that bit manipulation looks rather complex so I will take each significant statement one at a time. First a byte constant (HIBIT_MASK) was defined with just the high bit set. The code also declared working variables x and bc followed by a char array to act as a buffer for the Morse encoding.
The setup() function code then uses a loop to run through each element of both arrays. The longhand mCodes[] content is first sent to the Serial Monitor. The remaining code then addresses the values stored in the byte array. Each byte is copied in turn to the byte variable bc. The next part of the process is to find out how many code elements are included at the high end of the byte – so we need to read the number in the lower three bits. That count of significant bits is stored in the int variable x. After the char array is filled with zero char values with memset() that value in x is used to control the next loop which reads the high order bits in turn. If the bit is a zero then a dot is added to the code[] array, otherwise a dash. After each bit is read then the bits in the byte are shifted left bringing the next bit to position 7, ready to be compared to HIBIT_MASK. Once all of the significant bits have been translated to dots and dashes, the code[] array is displayed by the Serial Monitor.
The line if((bc & HIBIT_MASK) == 0) has the comment “take care with the brackets” as the == operator has higher precedence than the & operator. Without the extra brackets, the initial comparison would have been between the B10000000 value and 0 which would be false and thus the conditional test would always return false no matter what value was in the byte bc.
You might be wondering about the memset() function. This is one of the functions that can directly manipulate memory locations used in this chapter. It is found in the string.h library that is automatically made available to your Arduino programs. The functions in that library are documented in a later chapter.
Assuming the code test program output confirmed the code arrays were correct, we can go ahead and implement a program that will send a Morse code representation of some text using an LED or other output signal. First, we need to come up with some timings. There are supposedly an average of 4.79 letters in an English word. If we are going to transmit at a leisurely 20 words per minute that would be around 96 characters per minute.
The letter A as represented by Morse code would take 5+ units of time to send. 1 for the dot, 1 for the gap, 3 for the dash and then the inter-character gap.
I came up with a formula for calculating the length of a time unit (dot) based upon the average number of letters in a word and the relative frequency of the different letters in English and how they are represented in Morse code. It was:
timeUnit = 60000 / ((float)wordsPerMin * (4.79 * 9.08 + 6)); // time unit in milliseconds
However, it turns out there is a standard; well actually two standards. One is based upon repeating the word PARIS the relevant number of times in a minute and the other is based upon the word CODEX. As PARIS, in Morse code, has a near equal number of dots and dashes this looks like the preferred basis for a calculation. This results in a standard formula which is timeUnit = 1200 / wordsPerMin. Astonishingly, this produces a near identical result to my rather complex “back of an envelope” approach. This just goes to show that the early human Morse operators knew their trade and that I should not overthink these things.
Therefore 20 words per minute would be about 0.060 of a second per unit which is fast. If we were to downgrade our sending to the Scout test rate then we might get 0.242 of a second per unit. The Scout rate would have a dash lasting nearly three quarters of a second and I think I could cope with that but I suspect I might get bored during long messages. In fact, I ran most of my initial testing and debugging at a more realistic 40 words a minute.
The following program will send a string (stored in char array text[]) in Morse code using an attached LED or speaker or via a data pin – any or all three, at a rate set by the value of the const int wordsPerMin. If you want a breadboard diagram for the speaker then please refer to chapter 4 and the section “4.5 making a noise”. We can use the built in led for a visual signal.
#define HIBIT_MASK B10000000
#define C6 1047
const int SOUNDER = 3; // set pin values to zero if not required
const int LED_PIN = LED_BUILTIN;
const int DATA_PIN = 8;
enum CodePart {
dash, dot, space, letterSpace, wordSpace
};
const char text[] = "NOW IS THE TIME FOR ALL GOOD MEN TO COME TO OUR"
"AID";
const byte mCode[] = {
B01000010, B10000100, B10100100, B10000011, B00000001, B00100100,
B11000011, B00000100, B00000010, B01110100, B10100011, B01000100,
B11000010, B10000010, B11100011, B01100100, B11010100, B01000011,
B00000011, B10000001, B00100011, B00010100, B01100011, B10010100,
B10110100, B11000100, B11111101, B01111101, B00111101, B00011101,
B00001101, B00000101, B10000101, B11000101, B11100101, B11110101
};
const int wordsPerMin = 10;
unsigned long timeUnit = 0;
void setup() {
Serial.begin(115200);
if(LED_PIN > 0) {
pinMode(LED_PIN, OUTPUT);
}
if(DATA_PIN > 0) {
pinMode(DATA_PIN, OUTPUT);
digitalWrite(DATA_PIN, HIGH);
}
timeUnit = 1200 / wordsPerMin; // set time unit in milliseconds
Serial.println(timeUnit);
encode();
}
void loop() {
}
[N.B. later in this book you will meet the #ifdef compiler directive that could improve the way that the output options (LED, data and sound) are selected and included in this code.]
void encode() {
byte code;
bool blank = false;
for(int ci = 0; ci < sizeof(text); ci++) {
switch (text[ci]) {
case 'A'...'Z':
code = mCode[text[ci] - 65];
break;
case '0'...'9':
code = mCode[26 + text[ci] - 48];
case ' ':
blank = true;
break;
}
if(blank) {
send(wordSpace);
blank = false;
} else {
int bc = code & ((1 << 3)-1);
for(int bi = 0; bi < bc; bi++) {
if(bi > 0) {send(space);}
if((code & HIBIT_MASK) == 0){
send(dot);
} else {
send(dash);
}
code = code << 1;
}
send(letterSpace);
}
}
}
void send(CodePart codePart) {
unsigned long startMillis = millis();
unsigned long elapsedMillis = timeUnit;
switch(codePart) {
case dash:
elapsedMillis *= 3; // note drop through to dot: no break
case dot:
if(LED_PIN > 0) { digitalWrite(LED_PIN, HIGH);}
if(DATA_PIN > 0) {digitalWrite(DATA_PIN, LOW);}
if(SOUNDER > 0) {tone(SOUNDER, C6, elapsedMillis);}
break;
case letterSpace:
elapsedMillis *= 3;
break;
case wordSpace:
// double letter space but we have already sent one
elapsedMillis *= 3;
break;
}
while(true) {
if((unsigned long)(millis() - startMillis) >= elapsedMillis) {
break;
}
}
if(LED_PIN > 0) {digitalWrite(LED_PIN, LOW);}
if(DATA_PIN > 0) {digitalWrite(DATA_PIN, HIGH);}
}
The process looks up each non-space character from the text char array to get the Morse representation encoded in a byte. The code byte is then evaluated and the required dots, dashes and inter element spaces passed to the send() function which selectively flashes the LED, triggers a tone or pulls a data pin down to a LOW value (or maybe all three). After a time interval set by the word rate and Morse code element type, the LED is switched off and the data pin re-set HIGH.
When playing around with different word rates I found that my ability to differentiate between dots and dashes at higher rates based upon sound was just fine but that I had difficulty with the visual signals from the LED. Asking around showed that this was a normal “disability”. Students of evolutionary psychology might like to experiment with different LED colours for dots and dashes to see if that enhances human visual perception. I am not sure it would help but it might make for some interesting experiments.
The Morse sender option to signal via a data pin was set up to support the development of a Morse reading program. That program is rather more complex but writing relatively hard programs is a great way of enhancing our ability to write every day programs. By the way, it helps here to have a second Arduino available but as a Nano clone cost less than a high street coffee I hope that will not be too much of a barrier to progress.
Reading Morse
To keep things nice and simple we can use an external interrupt to capture an incoming Morse code signal. We will need to respond to changes from LOW to HIGH and from HIGH to LOW. The data pin could be attached to almost anything used to collect an incoming signal for evaluation but we can use another Arduino running the program we developed to send a Morse signal. This does rather require a second available board – a Nano would be great although two Unos are shown here. The Arduino on the right is running our send Morse program and this can be restarted when required by pressing the reset button. I linked the earth pins on both boards as well as connecting the two data pins.
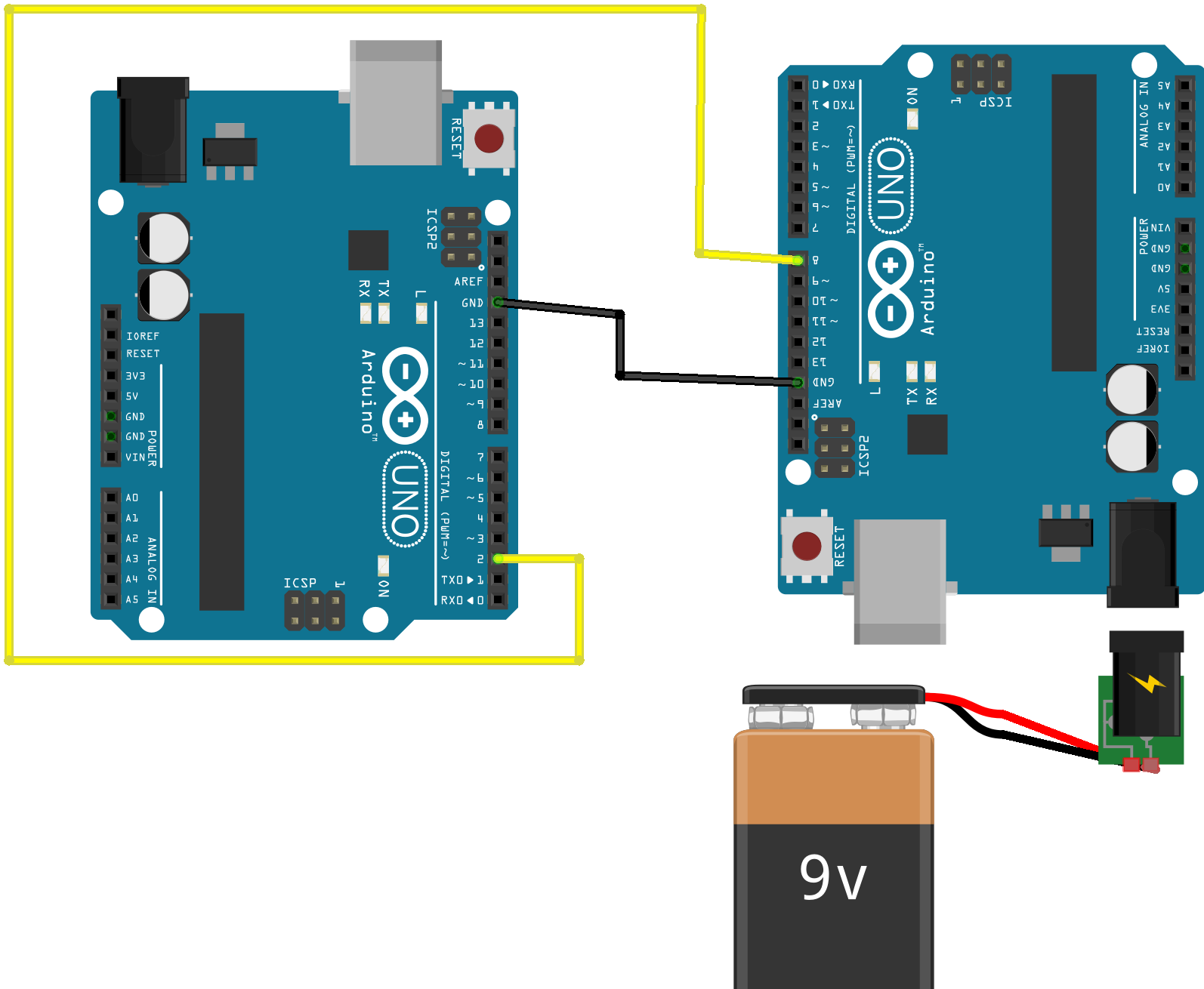
The Morse reading program will need to capture the time between the start and end of each signal element and (as we know) these are all relative to each other. We will need to time the “beeps” and the gaps between the “beeps” to make sense of the signal.
Our second program could start with:
#include <util/atomic.h>
const int MORSE_PIN = 2; // External interrupt 0
struct SignalInt {
bool isCode = false;
unsigned long intTime = 0;
};
volatile int signalCount = -1;
int countCopy = 0;
SignalInt testSignals[60];
unsigned long lastMicros = micros();
The code defines a struct to hold signal information. This includes a Boolean where true represents a “beep” and false represents a gap. There is also an array of those structs that we can use to test the process of capturing a Morse signal.
void setup() {
Serial.begin(115200);
pinMode(MORSE_PIN, INPUT_PULLUP);
noInterrupts();
attachInterrupt(digitalPinToInterrupt(MORSE_PIN),morseInter,CHANGE);
interrupts();
}
Our initial setup() function simply needs to ready the chosen pin and attach any CHANGE interrupts to a function named morseInter(). That function records pin interrupts following on from the first change to LOW in a struct added to the testSignals[] array.
void morseInter() {
unsigned long currentMicros = micros();
bool pinLow = (digitalRead(MORSE_PIN) == LOW);
if(signalCount == -1 && !pinLow) {return;}
if(signalCount >= 0) {
testSignals[signalCount].intTime =
(unsigned long)(currentMicros - lastMicros);
}
lastMicros = currentMicros;
signalCount++;
testSignals[signalCount].isCode = pinLow;
// pinLow flags a code element rather than an interval
}
void loop() {
ATOMIC_BLOCK(ATOMIC_RESTORESTATE){
countCopy = signalCount;
}
if(countCopy > 59) {
detachInterrupt(digitalPinToInterrupt(MORSE_PIN));
analyse();
signalCount = -1; // stop
}
}
void analyse() {
for(int i=0; i<60;i++) {
Serial.print(testSignals[i].isCode);
Serial.print(": ");
Serial.println(testSignals[i].intTime);
}
}
The code sets up an external interrupt on pin 2. The interrupt calls the ISR morseInter(). The ISR waits for the data pin to be pulled LOW for the first time and then starts saving the pin state and timings in an array of structs called testSignals[]. Each struct just holds a bool value to indicate if it represents a possible dash or dot and the time duration of those signals and the inter signal periods (when the pin is HIGH). The loop() function monitors the count of data items collected and stops the data collection when the sampling array is full. The analyse() function at this stage simply displays the values in the testSignals[] array using the Serial Monitor.
We can use the displayed values to check the program is collecting results that look like Morse code. I ran the Morse sending program at 40 words per minute so expected to see signal times that were multiples of 30 milliseconds (12000 / 40). The test string started “NOW IS THE” and so I expected to see the first signal value indicating a dash and then a space and then a dot. I was encouraged by the relative length of the two first signal elements and by the following three which again looked like dashes (hopefully the letter O).
1: 89988 0: 30708 1: 29664 0: 90060 1: 90028 0: 29688 1: 90028 0: 29688 1: 90028 0: 90060
There is clearly some variability in the captured times that could stem from the transmission rate and from the signal capture. If the code is going to reliably read an incoming Morse signal then some small allowances will need to be made.
We could use an enum to enumerate the different code elements and then a struct to hold a range of times. We can then use an array of times for each element.
enum CodePart {
dot, dash, space, letterSpace, wordSpace
};
struct CodeTimes {
int minMillis;
int maxMillis;
};
CodeTimes codeTimes[] = {
{0, 0}, {0, 0}, {0, 0}, {0, 0}, {0, 0}
};
Once added to the program a function can then be used to calculate the values based upon the expected word rate which could be defined near the top of the code (#define WORD_RATE 40 ). The CodePart enum is used here as documentation – “dash” is more meaningful when you read the code than “1”.
void setDefaults() {
int dotTime = 1200 / WORD_RATE;
codeTimes[dot].minMillis = codeTimes[space].minMillis = dotTime - 2;
codeTimes[dot].maxMillis = codeTimes[space].maxMillis = dotTime + 2;
codeTimes[dash].minMillis = codeTimes[letterSpace].minMillis =
dotTime * 3 - 2;
codeTimes[dash].maxMillis = codeTimes[letterSpace].maxMillis =
dotTime * 3 + 2;
codeTimes[wordSpace].minMillis = dotTime * 6 - 2;
codeTimes[wordSpace].maxMillis = dotTime * 6 + 2;
}
If we put a call to that function near the top of setup() then we could change the analyse() function to try out those ranges.
void analyse() {
for(int i=0; i<60;i++) {
long millTime = testSignals[i].intTime / 1000;
if(testSignals[i].isCode) {
if(millTime >= codeTimes[dot].minMillis &&
millTime <= codeTimes[dot].maxMillis) {
Serial.println("dot");
}else if(millTime >= codeTimes[dash].minMillis &&
millTime <= codeTimes[dash].maxMillis) {
Serial.println("dash");
} else {
Serial.print("Unknown Signal: ");
Serial.println(millTime);
}
} else {
if(millTime >= codeTimes[letterSpace].minMillis &&
millTime <= codeTimes[letterSpace].maxMillis) {
Serial.println("End of letter");
} else if(millTime >= codeTimes[wordSpace].minMillis &&
millTime <= codeTimes[wordSpace].maxMillis) {
Serial.println("End of word");
}
}
}
}
The microseconds are divided by 1000 and then compared to the time ranges in milliseconds calculated in setDefaults().
When run, I saw the following output which indicated that Morse code letters and words were correctly identified.
dash dot End of letter dash dash dash End of letter dot dash dash End of word dot dot End of letter dot dot dot End of word
Based upon the analysis of that sample, the code could next move on to translating the values in the testSignals[] array into human sensible text. The legendary Charles Petzold famous for writing a book that taught a generation of programmers to write Windows programs (in C++) also wrote the book, mentioned previously, called “Code – the hidden language of computer hardware and software”. In that book, the author pointed out that it was possible to encode a Morse signal as a stream of bits. He noted that a dot could be represented as a bit set to 1 and a dash (being three times the length of a dot) could be represented as three bits set to 1. The “spaces” could all be represented as sequences of bits set 0. Using that approach, the Morse encoding of the word “Morse” could be represented as a stream of bits
1110111000111011101110001011101000101010001
This is an interesting way of encoding Morse as a binary sequence given that there are 5 different components that are “collapsed” neatly into just two values with the time element represented by repetition. Unfortunately, I could not see how this technique would compress a sequence of Morse characters any more efficiently than our original “byte” format.
So, not wishing to be diverted, I set up a generous 30 element byte array I called readCodes[] to hold the Morse codes (in our byte format). The individual bytes are formed by effectively reversing the process used to generate the code at the send end from our master Morse code table. The function readBytes() runs through our array of testSignals[] and translates the code values into our compressed byte format.
void readBytes() {
int cCount = 0;
int bCount = 0;
byte wrk = B00000000;
unsigned long thisTime;
for(int i = 0; i < 60; i++) {
thisTime = testSignals[i].intTime / 1000;
if(testSignals[i].isCode) {
wrk = wrk << 1;
if(thisTime >= codeTimes[1].minMillis && thisTime <=
codeTimes[1].maxMillis) {
wrk ^= 1;
}
bCount++;
} else {
if(thisTime >= codeTimes[3].minMillis) {
wrk = wrk << (8 - bCount);
wrk ^= bCount;
bCount = 0;
readCodes[cCount] = wrk;
cCount++;
wrk = B00000000;
if(thisTime >= codeTimes[4].minMillis && thisTime <=
codeTimes[4].maxMillis) {
readCodes[cCount] = wrk;
cCount++;
}
}
}
}
}
The next function showCode() takes the array of encoded byte values and translates them to text. OK there is a cheat here to keep the code short as it only translates letters but we can do a more complete job later after some other structural changes. For this to work you need to copy the mCode[] byte array from the Morse sending program.
void showCode() {
for(int i = 0; i < sizeof(readCodes); i++) {
if(readCodes[i] == B00000000) {
if(i > 0 and readCodes[i-1] == B00000000) {
break;
}
Serial.println(" ");
} else {
for(int j = 0; j < 26; j++) {
if(mCode[j] == readCodes[i]) {
Serial.print((char)(65 + j));
break;
}
}
}
}
}
If we comment out the call to analyse() in the loop() function we can add calls to readBytes() and showCode() in its place. Now the program should be ready for another test run.
What I saw was “NOW IS THE TIME F” which were the letters encoded in the first 60 time values read by the interrupt ISR.
We have now tested a few ideas with some “just about good enough” functions. This helps confirm the basic strategy and gives us confidence that we can write the better structured program required to translate a more meaningful stream of Morse.
A properly effective program needs to be able to accept one or more Morse “transmission” of arbitrary length without an undue impact upon the available memory. The strategy needs therefore to up the pace a bit. Instead of a fixed length array to store the incoming signal we need a data structure that can expand and contract. The code needs to be able to evaluate the contents of that structure to extract the code elements ready for translation into text. Our target is to manage those processes quickly and as efficiently as possible.
A FiFo Queue
So let’s sharpen our pointers and implement something called a queue that can have a variable size unlike an array. This is, of course, risky within the limited memory allocation of an Arduino but the intention is to remove items from the queue as promptly as possible and (eventually) while the queue is still being added to.
This queue type is called a FiFo queue as records are added at the tail end and read from the start – First In, is always First Out. The other common queue type is LiFo (Last In, First out) that acts just like a software “stack”.
We can start by modifying the struct called SignalInt so that it includes a pointer to its own type. We can use that to point to following members of a queue. We also need a struct for the key components of the queue with a pointer and a status byte to replace the simple count of signal elements received.
struct SignalInt {
bool isCode = false;
unsigned long intTime = 0;
struct SignalInt* next;
};
struct SignalQueue {
struct SignalInt* head;
struct SignalInt* tail;
int count;
};
struct SignalQueue* signalQ = NULL;
volatile byte sStatus = 0; // signal status
We can also go ahead and remove the testSignals[] array and the associated counts. Having done its job, the analyse() function is also now surplus to requirements. Now back to building the queue.
The newQueue() function allocates enough memory in the Arduino heap for a SignalQueue struct and returns a pointer to that memory allocation after initialising the head and tail values to NULL. The memory is allocated using the malloc() function. The malloc() function is passed the number of bytes to reserve from the heap and it returns a pointer to the reserved memory location.
struct SignalQueue* newQueue() {
struct SignalQueue* p = malloc(sizeof(*p));
p->head = p->tail = NULL;
p->count = 0;
return p;
}
You might argue that this code does not create an instance of the struct in question. In some ways you would be right as all we have is a chunk of memory that we are going to treat as an instance of the struct even though all we have is a pointer to it. Maybe that is all any data item is; it is just that some have a variable name as well as a pointer.
As this is a dedicated queue for storing SignalInt structs the function queueAdd can be passed the values isCode and intTime to initialise a new entry. Again, memory is allocated in the heap for this struct instance and the pointer returned by malloc() used to update either the queue head or the previous queue end record. The queue tail value is always updated to point to the newest entry in the queue. The malloc() function is designed to be as efficient as possible. If we get to the stage where we can remove elements from the head of the queue while new ones are still being added then malloc() will allocate memory for new items where it has been freed after being previously used. Where a data item is located in memory is unimportant as it is always going to be directly accessed by its address.
bool queueAdd(const bool isCode, const long intTime) {
struct SignalInt* p = malloc(sizeof(*p));
if(p == NULL) {return false;}
p->isCode = isCode;
p->intTime = intTime;
p->next = NULL;
if(signalQ->head == NULL) {
//queue is empty so update both ends
signalQ->head = signalQ->tail = p;
} else {
signalQ->tail->next = p; // update the previous last item in Q
signalQ->tail = p; // update the Q tail
}
signalQ->count++; // increment the count of Q items
return true;
}
Take your time with the pointers and it will all make sense. In fact, the “arrow notation” helps by making the pointer look more like a variable name in the code.
Continuing with our queue, all we need now is a way to retrieve a pointer to the first record (if any) in the queue plus a way to remove the first record in the queue and to recover the allocated memory. The aim here is that when the data in the queue has been processed then all of the memory used should have been recovered and made available to other functions running on our Arduino.
struct SignalInt* readFirst() {
return signalQ->head;
}
bool deQueue() {
if(signalQ->head == NULL) {return false;}
struct SignalInt* h = signalQ->head;
struct SignalInt* n = h->next;
free(h);
signalQ->head = n;
signalQ->count--;
return true;
}
The free() function is used to recover a heap memory block allocated by the malloc() function. The free() function simply needs to be passed the pointer to that memory location. The free() function knows how much memory to mark as free based upon a table of allocated memory spaces maintained by the malloc() function.
We now have a prototype for a data structure that, with minimal modification, should be able to handle any sort of incoming data that can’t be processed immediately upon arrival in any program. To test it out, we need to make a few modifications to some existing functions but we also have to build in some way of recognising that a Morse code message has reached an end.
One choice was to double down on the interrupt theme and use a timer that could be regularly re-set by the ISR dealing with the incoming data but trigger “message end” when finally a timer interrupt was allowed to occur. You can refer to the chapter on timers for more details of the options available there.
Timer1 makes a good choice but if that was already employed doing something else then a Watchdog timer might be just the thing as that will happily support time intervals as long as 8 seconds. The timer can be initialised with a function (or directly in the setup function of course).
void setupTimer() {
TCCR1A = 0; // Timer control register
TCCR1B = 0;
TCNT1 = 3036; // start value 65536 - (16Mhz / 256)
TCCR1B |= (1 << CS12); // 256 prescaler
TIMSK1 |= (1 << TOIE1); // set timer overflow interrupt
}
With an ISR set to keep restarting the timer when the signal status is 0 and otherwise to mark the end of the signal since a second had passed since the last pin interrupt (assuming we reset the timer in the relevant ISR – coming up next).
ISR(TIMER1_OVF_vect){
byte cStatus = sStatus;
switch (cStatus){
case 0:
TCNT1 = 3036; // not started yet so reset timer
break;
case 1:
sStatus = 2; // no items added to Q in last second
break;
}
}
The morseInter() function now places the incoming signal records in the queue rather than the array previously used, It also resets the timer.
void morseInter() {
static bool wasCode;
unsigned long currentMicros = micros();
bool pinLow = (digitalRead(MORSE_PIN) == LOW);
if(sStatus == 0 && !pinLow) {return;}
if(sStatus == 0) {
TCNT1 = 3036; // reset before status change
sStatus = 1; // signal started
} else {
if(queueAdd(wasCode, ((unsigned long)(currentMicros -
lastMicros)) / 1000)) {
TCNT1 = 3036; // reset timer
} else {
sStatus = 2; // error adding to Q so stop
}
}
lastMicros = currentMicros;
wasCode = pinLow;
}
The readBytes() function now needs to consume queue entries (not forgetting to delete them) but is otherwise unchanged.
void readBytes() {
int cCount = 0;
int bCount = 0;
byte wrk = B00000000;
while(signalQ->count) {
SignalInt* item = readFirst();
long t = item->intTime;
if(item->isCode) {
wrk = wrk << 1;
if(t >= codeTimes[dash].minMillis &&
t <= codeTimes[dash].maxMillis) {
wrk ^= 1;
}
bCount++;
} else {
if(t >= codeTimes[letterSpace].minMillis) {
wrk = wrk << (8 - bCount);
wrk ^= bCount;
bCount = 0;
readCodes[cCount] = wrk;
cCount++;
wrk = B00000000;
if(t >= codeTimes[wordSpace].minMillis &&
t <= codeTimes[wordSpace].maxMillis){
readCodes[cCount] = wrk;
cCount++;
}
}
}
deQueue();
}
}
The setup() function needs to make sure the queue is initialised and that the timer is started.
void setup() {
Serial.begin(115200);
setDefaults();
signalQ = newQueue();
pinMode(MORSE_PIN, INPUT_PULLUP);
noInterrupts();
attachInterrupt(digitalPinToInterrupt(MORSE_PIN),morseInter,CHANGE);
setupTimer();
interrupts();
Serial.println("Ready");
}
The loop() function can be shortened and the #include for atomic.h removed from the program.
void loop() {
if(sStatus == 2) {
detachInterrupt(digitalPinToInterrupt(MORSE_PIN));
sStatus = 0;
readBytes();
showCode();
}
}
The program should now be ready to retest with a short test message from the sendMorse program running on the companion Arduino.
Hopefully, you are now buoyed up by success and maybe wondering about that readCodes[] array. Surely that could also be replaced by a queue structure? It would often make sense to replace fixed arrays with a suitable data structure like a queue when it is unclear just how many elements are going to be stored at any one time. We could design a generic queue where each instance could take an alternate data type. However, in this program we have an issue that derives from malloc(). That code is not “re-entrant”. This means that we can’t have a situation where our code is using malloc() to allocate some memory when there is the risk that an interrupt will occur and also call malloc(). The result would be unpredictable and would probably lead to software failure. We will need to look for a way around this in order to deal with messages of arbitrary length.
First though, we could explore the part of this program that interprets the encoded Morse bytes created by analysing the signals received by the external interrupt ISR. In the context of interpreting Morse then it is not impractical to just loop through the same list of bytes used by the SendMorse program. However, we can usefully explore some alternative approaches here.
The advantage of just looping through the Morse byte array is that the actual alpha or numeric character we are seeking is implicit in the location of any match within that array. The search time should average out at about half the number of array elements – so the search time should be n/2 over a reasonable sample where n is the length of the byte array. Can we beat that? Yes we can, and beating that time might be significant in other projects where the number of items we wanted to search was large and/or the lookup was time critical.
Binary Tree Structure
Many people learning Morse code are introduced to this diagram of the code laid out in a way that makes decoding a sequence of dots and dashes very straightforward.
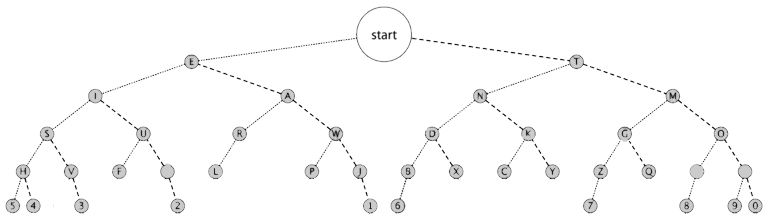
From the start, you navigate the paths based upon the next element of a Morse code. If it is a dot you move left and if it is a dash you move right. When all of the dots and dashes of a character have been used then stop, as the circle you have arrived at is the correct translation. The structure of the diagram is reminiscent of a branching tree and there are a maximum of two choices stemming from any branching point – hence binary tree. It just turns out that binary trees are a classic structure in computer science.
Using a structure like this, our Morse code elements can always be translated with a maximum of 5 reads and with the most common letters (in English anyway) turning up in just 1, 2 or 3 reads. This is way more efficient than an exhaustive search of the options.
Another approach would be to organise a lookup list in encoded byte order and then use a binary search to find the required match. This would require a maximum of Log2n reads which I calculate to be 5.17 – so probably 5. This is equivalent to the binary tree except that the binary tree (in this instance) is favorably biased towards the most common letters. The chapter on sorts should provide you with the required resources should you choose binary search as a lookup strategy. For the purposes of this program, we should probably focus on the binary tree.
Binary trees are very effective lookup structures and a later section of this chapter will build a generic tree suitable for general purpose use. However, binary trees need to be well balanced. That is the entries to the left of a given choice point should be balanced by a near equal number on the right. This can present a challenge when populating such a tree structure. In the instance of the Morse code lookup tree we can see from the diagram that it is fully balanced and has a fixed number of entries. This means that we can implement this tree within an array and that array can replace the mCode[] array in our program. I am sure that you will agree that typing in the mCode[] array was a touch tedious so I am proposing that we use another Arduino program to write this new one for us.
So start a new program in the IDE and (perhaps) call it “BinaryTreeBuilder”. It needs to start with #define HIBIT_MASK B10000000 just like the SendMorse program together with the now very familiar mCode[] array – so copy and paste. We need to sort the mCode[] array values and their translations before we can build our binary tree. This will need a suitable struct and an array.
struct Lookup
{
byte code;
char result;
};
struct Lookup bSearch[36];
We will also need an array to hold the tree and a struct for the tree entries.
struct Node
{
byte left;
byte right;
char result;
};
struct Node bTree[40];
The createCodeArray() function copies the bytes and translations from the mCode[] array to the bSearch[] array.
void createCodeArray() {
for(int i = 0; i < 36; i++) {
bSearch[i].code = mCode[i];
bSearch[i].result = (i < 26) ? (char)(i + 65) :
(char)(i + 22);
}
}
The bSearch[] array next needs to be sorted so how about a custom quick sort as laid out in a previous chapter? This one is designed to use pointer arithmetic instead of array index values – just as a little exercise.
// a quick sort for the bSearch array Lookup structs
// makes use of pointer arithmatic (just for fun)
void bSort(Lookup array[], int left, int right) {
if(left > right) {return;}
swapB(array + left, array + ((left + right) / 2));
int last = left;
for(int i = left + 1; i <= right; i++) {
if(compB(array + i, array + left) < 0) {
swapB(array + (++last), array + i);
}
}
swapB(array + left, array + last);
bSort(array, left, last - 1);
bSort(array, last + 1, right);
}
The sort needs a comparison function and a swap function of course.
int compB(Lookup* a, Lookup* b) {
if(a->code == b->code) {return 0;}
return (a->code > b->code) ? 1 : -1;
}
void swapB(Lookup* a, Lookup* b) {
Lookup temp = *a;
*a = *b;
*b = temp;
}
Once the bSearch array is sorted into byte order rather than code translation order we can use the values to populate the binary tree.
void createBinaryTree() {
for(int i = 0; i < 40; i++) {
bTree[i].result = ' ';
}
int bIndex = 0;
for(int i = 0; i < 36; i++) {
bIndex = 0; // start at the beginning
byte code = bSearch[i].code;
int bc = code & ((1 << 3)-1);
for(int bi = 0; bi < bc; bi++) {
if((code & HIBIT_MASK) == 0){
// dot
if(bTree[bIndex].left == 0) {
bTree[bIndex].left = nextFree();
}
bIndex = bTree[bIndex].left;
} else {
if(bTree[bIndex].right == 0) {
bTree[bIndex].right = nextFree();
}
bIndex = bTree[bIndex].right;
}
code = code << 1;
}
bTree[bIndex].result = bSearch[i].result;
}
}
That code pushes dot values down the left hand leg from any given position and dash values down the right hand leg. The nextFree() function returns the next available entry in the array which has some parallel with malloc() being used to find an available memory location in the heap. The function nextFree() though is very simple.
byte nextFree() {
static byte nFree = 0;
return ++nFree;
}
Once the tree is constructed we will need a function to find any given code byte in that tree and return the translation. We can use this to test our binary tree and we will be copying it back into our Morse reading program.
char treeSearch(byte findThis) {
int treeIndex = 0;
int bc = findThis & ((1 << 3)-1);
for(int bi = 0; bi < bc; bi++) {
if((findThis & HIBIT_MASK) == 0){
treeIndex = bTree[treeIndex].left;
} else {
treeIndex = bTree[treeIndex].right;
}
findThis = findThis << 1;
}
return bTree[treeIndex].result;
}
The displayTreeCode() function is what we have been working towards as it is designed to output a line of C code that defines the tree array to the serial monitor.
void displayTreeCode() {
Serial.print("const Node bTree[] = {");
for(int i = 0; i < 40; i++) {
Serial.print((i > 0) ? ", {" : "{");
Serial.print(bTree[i].left);
Serial.print(", ");
Serial.print(bTree[i].right);
Serial.print(", '");
Serial.print(bTree[i].result);
Serial.print("'}");
}
Serial.println("};");
}
Now a function to check that the tree works follows.
void testTree() {
Serial.println("Testing binary tree");
for(int i = 0; i < 36; i++) {
Serial.print((i < 26) ? (char)(i + 65) : (char)( i + 22));
Serial.print(" : ");
char getC = treeSearch(mCode[i]);
Serial.println(getC);
}
}
The setup() function can get everything done in the correct order.
void setup() {
Serial.begin(115200);
createCodeArray(); // load codes into bSearch
bSort(bSearch, 0, 35); // sort the array
createBinaryTree();
displayTreeCode();
testTree();
}
Coming clean, that did take a while but then again setting up the binary tree would have been a fiddly job. Plus we got to test a lookup function to use the tree and we had all the fun of just writing C code to run on an Arduino. No downside?
The first line of output to the serial monitor will need copying and pasting into the Morse reading program to replace the mCode[] array along with the treeSearch() function. The program will also need the HIBIT_MASK definition and the declaration of the node struct. The tree code should look something like the following once you have tidied it up a bit.
const Node bTree[] = {{1, 20, ' '}, {2, 13, 'E'}, {3, 9, 'I'},
{4, 7, 'S'}, {5, 6, 'H'}, {0, 0, '5'},
{0, 0, '4'}, {0, 8, 'V'}, {0, 0, '3'},
{10, 11, 'U'}, {0, 0, 'F'}, {0, 12, ' '},
{0, 0, '2'}, {14, 16, 'A'}, {15, 0, 'R'},
{0, 0, 'L'}, {17, 18, 'W'}, {0, 0, 'P'},
{0, 19, 'J'}, {0, 0, '1'}, {21, 29, 'T'},
{22, 26, 'N'}, {23, 25, 'D'}, {24, 0, 'B'},
{0, 0, '6'}, {0, 0, 'X'}, {27, 28, 'K'},
{0, 0, 'C'}, {0, 0, 'Y'}, {30, 34, 'M'},
{31, 33, 'G'}, {32, 0, 'Z'}, {0, 0, '7'},
{0, 0, 'Q'}, {35, 37, 'O'}, {36, 0, ' '},
{0, 0, '8'}, {38, 39, ' '}, {0, 0, '9'},
{0, 0, '0'}};
With all that in place, you can tweak the showCode() function and rerun the Morse reader test to ensure it is all properly in place.
void showCode() {
for(int i = 0, j = sizeof(readCodes); i < j; i++) {
if(readCodes[i] == B00000000) {
if(i > 0 and readCodes[i-1] == B00000000) {
break;
}
Serial.println(" ");
} else {
Serial.print(treeSearch(readCodes[i]));
}
}
}
Given that the program can now decode a given Morse character at least three times faster than before we can have a stab at starting the translation of Morse to text while a message is still being received. This requires some tweaks to the readBytes() and showCode() functions to add an optional control over how much of the available data they process plus a change to the loop() function to allow it to control the early data processing. We also need to do something with the readCodes[] array to get it to act a bit like a queue. Starting there, we can add a #define for the size of the array, an int variable to point to the next available position in the array and a new function to “roll” the array items down to replace the first element once we have sent that character to the Serial Monitor. So add the following to the program.
#define CODE_LIMIT 30
byte readCodes[CODE_LIMIT];
int nextCode = 0;
void rollCodes() {
nextCode--;
for(int i = 0; i < nextCode; i++) {
readCodes[i] = readCodes[i+1];
}
}
The showCode() function can be passed a bool parameter to say if it should display all of the current content of the readCodes[] array up to the index nextCode or just the first character.
void showCode(bool all) {
for(int i = 0; i < nextCode; i++) {
if(readCodes[i] == B00000000) {
Serial.println(" ");
} else {
Serial.print(treeSearch(readCodes[i]));
}
if(!all) {return;}
}
nextCode = 0;
}
The readBytes() function also gets a bool parameter that (for no particular reason) seems to work the other way around to the one above. This one can be used to force a return after processing a complete Morse character code. The whole function is shown here but you just need to make the changes.
void readBytes(bool justOne) {
bool codeAdded = false;
int bCount = 0;
byte wrk = B00000000;
while(signalQ->count) {
SignalInt* item = readFirst();
long t = item->intTime;
if(item->isCode) {
wrk = wrk << 1;
if(t >= codeTimes[dash].minMillis &&
t <= codeTimes[dash].maxMillis) {
wrk ^= 1;
}
bCount++;
} else {
if(t >= codeTimes[letterSpace].minMillis) {
wrk = wrk << (8 - bCount);
wrk ^= bCount;
bCount = 0;
readCodes[nextCode] = wrk;
codeAdded = true;
nextCode++;
wrk = B00000000;
if(t >= codeTimes[wordSpace].minMillis &&
t <= codeTimes[wordSpace].maxMillis){
readCodes[nextCode] = wrk;
nextCode++;
}
}
}
deQueue();
if((justOne && codeAdded) || nextCode > CODE_LIMIT - 1) {break;}
}
}
Now the loop() function can be used to start processing Morse signals in the queue (and displaying their translation) while the message is still being received. So having shortened it we now need to expand it a bit.
void loop() {
switch(sStatus) {
case 2:
detachInterrupt(digitalPinToInterrupt(MORSE_PIN));
sStatus = 0;
while(signalQ->count > 0 || nextCode > 0) {
readBytes(false);
while(nextCode > 0) {
showCode(true); // display all characters in array
}
}
attachInterrupt(digitalPinToInterrupt(MORSE_PIN),morseInter,CHANGE);
Serial.println("Ready for more");
break;
case 1:
if(signalQ->count >=11 && nextCode < CODE_LIMIT - 2) {
readBytes(true); // read a character from signal stream
}
if(nextCode > 0) {
showCode(false); // display top character
rollCodes(); // roll it off the array
}
break;
}
}
When the sStatus flag is set to show an incoming message the function calls readBytes() when there are at least a minimum number of items in the signal queue and there is room in the readCodes[] array. This call is followed by a call to showCode() to display the first character in the array and to then roll it off leaving any other characters in place.
The process for when the status flag changes to “2” has also been changed to temporarily halt any external interrupts and to then process and display all remaining signal values. The external interrupt can then be re-enabled ready to accept a new message.
Give it a try. I found that the process running on a UNO kept reasonable pace with an incoming Morse rate of 40 words a minute. Not bad, when the external interrupt processing is being triggered every 30 or 60 milliseconds.
Can we improve the efficiency of our data storage further? A review of the readBytes() function shows that the very necessary signal element that marks the space between dots and dashes is not required by subsequent processing. We could stop adding that item to the queue and reduce our queue data storage requirement by nearly 50%. A code change in morseInter() would do the trick.
} else {
int t = (unsigned long)(currentMicros -
lastMicros) / 1000;
if(wasCode || t >= codeTimes[letterSpace].minMillis) {
if(queueAdd(wasCode, t)) {
TCNT1 = 3036; // reset timer
} else {
sStatus = 2; // error adding to Q so stop
}
}
I am sure you can see where to apply that change. With that added, you can also then change the minimum number of queue items required to try and process a Morse character from 11 to 6 in the loop() function.
Developing that program was a process of continuous improvement that ended up with an efficient code base running well on a relatively slow microprocessor with very limited SRAM.
We can next have another look at FiFo queue structures and full blown Binary Trees.
Code downloads for this chapter are available here.