Chapter 2: Binary Computers
It is highly likely that you have seen an image of a computer chip that exposes some of the fine detail and organisation of the microscopic components contributing to the function of these extraordinary and revolutionary devices.

They look astonishingly complex and near impossible to understand and yet, at heart, they are simple devices constructed from a small range of component types and with an equally small repertoire of fundamental capabilities. If you have a hankering to understand just how a computer is constructed and just how that construction allows it to be programmable then I would recommend reading a book called “CODE the hidden language of computer hardware and software” by Charles Petzold. The book was written in the late nineteen nineties when CDs were still cool and many things still recorded on tape but don’t let that put you off, this book explains how a collection of simple switches can be organised so that they will execute instructions (that are themselves just numbers) and deliver a working computer.
Our desktop or laptop computers are binary computers. This means that everything is represented within our computers as a number made up of just two digits. To us humans brought up from babyhood counting with a number system based upon 10, a binary number system sounds like an unnecessary complication. However, when it comes to constructing a computer, a binary system is a massive simplification. Binary computers can use a high voltage (actually very low, maybe 3.3 or 5 volts) to denote one digit and a zero voltage to denote the other.
Number Bases
If you are unfamiliar with number systems (binary in particular) other than the one we were all taught as a child then it will help your understanding of programming and the Arduino greatly to read through the following (brief I promise) introduction.
There is a general assumption that our number system is based upon 10 because most of us have 10 fingers and our fingers would be a logical start point for counting things. On that basis, a world of cartoon characters would probably have a number system based upon 8 and if (say) dolphins have developed a number system then it might well be based upon 2 like our computers. The chances are high that any alien species in other parts of our galaxy would have a number system based upon their own anatomy. There is no universal law that says 10 is a better system than any other, it just seems the most obvious to us humans.
When we come to write our decimal (base 10) numbers down we find that we only need symbols to represent the digits 0 through 9. This is because the way we represent numbers is a place based system. When we see the number 123 written down we understand that the 1 represents one hundred and this is a greater quantity than the next digit 2 which is also representing a greater quantity (twenty) than the last digit 3. The relative position of each digit tells us what it represents.
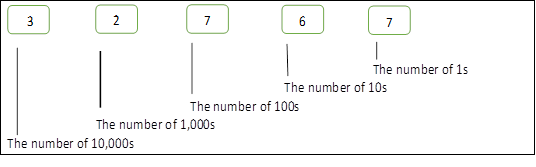
If we wrote down the number 32767, we would know that the 3 represented 3 x 10,000 and the 2 represented 2 x 1,000 and so on to the final 7 which represents 7 x 1. We could also express those position multipliers as powers of 10.
| 3 | 3 x 10,000 | 3 x 104 |
| 2 | 2 x 1,000 | 3 x 103 |
| 7 | 7 x 100 | 7 x 102 |
| 6 | 6 x 10 | 6 x 101 |
| 7 | 7 x 1 | 7 x 100 |
(Any number to the power of zero is one by the way.)
A notional cartoon character number system would only need the digits 0 through 7 and a similar position rule could be applied. Numbers base 8 are known as octal.
| 3 | 3 x 4,096 | 3 x 84 |
| 2 | 2 x 512 | 2 x 83 |
| 7 | 7 x 64 | 7 x 82 |
| 6 | 6 x 8 | 6 x 81 |
| 7 | 7 x 1 | 7 x 80 |
The number 32767 base 8 represents a smaller quantity than 32767 base 10. I am sure that you can quickly calculate that 32767 base 8 would represent the same value as 13,815 base 10. With a bit more work you might calculate that 32767 base 10 would be represented by the number 77777 base 8.
If the position of a digit in a number tells us how much to multiply that digit by and that this can always be represented as a power of the number base, how would things look for a base 2 system where we only have the digits 0 and 1.
| 1 | 1 x 128 | 1 x 27 |
| 0 | 0 x 64 | 0 x 26 |
| 1 | 1 x 32 | 1 x 25 |
| 0 | 0 x 16 | 0 x 24 |
| 1 | 1 x 8 | 1 x 23 |
| 1 | 1 x 4 | 1 x 22 |
| 1 | 1 x 2 | 1 x 21 |
| 1 | 1 x 1 | 1 x 20 |
I hope it is clear that it can work just the same – we just need a few more characters to represent larger numbers. The number 10101111 in binary would be represented as 257 in octal and 175 base 10 (decimal).
Binary Arithmatic
How does a binary system work when you need to do arithmetic? Well addition is pretty straightforward. 0 plus 0 is 0. 0 plus 1 is 1 and 1 plus 1 is 0 carry 1. So
1011001
+ 10101
-----------
1101110
Multiplication is even simpler. Multiply any digit by 0 and the result is 0. Multiply any digit by 1 and it stays the same.
1101
x 1011
------------
1101
1101
0000
1101
==========
10001111
Suppose we had evolved with 8 digits rather than 5 on each hand? If we ignore the challenge this might have given professional cartoonists, we might surmise that humans with that many fingers and thumbs would have developed a counting system with a number base 16. In fact, base 16 is a very handy number base for programmers and it is known as hexadecimal. A byte (8 binary digits) is easily represented by two hexadecimal digits and two characters are lot simpler to remember and to type correctly into a program than 8 zeros and ones.
A hexadecimal number system clearly needs symbols to represent numbers from zero to fifteen. Being a naturally decimal species we only have values for zero to nine so programmers have had to call on the services of the letters a to f to fill in for the missing characters. The next table is a bit more challenging as it uses two of the additional symbols for decimal values 10 through 15.
| E | E x 4096 | E x 163 | In decimal 14 x 163 |
| 7 | 7 x 256 | 7 x 162 | |
| C | C x 16 | C x 161 | In decimal 12 x 161 |
| 1 | 1 x 1 | 1 x 160 |
e7c1 (upper or lower case is optional) in hexadecimal, would be represented as 59,329 in decimal.
Hexadecimal FF (or ff) would be represented as 255 in decimal or 11111111 in binary.
Converting values between binary, octal, decimal and hexadecimal is reasonably straightforward but if you are using a Windows 10 (or later) computer to program your Arduino then the built in Calculator app has a “Programmer” option that does it all for you as well as calculating arithmetic in those different number bases.
Within a binary computer, all data is represented as a sequence of binary digits. Each binary digit is called a bit and bits are organised as bytes with each byte being constructed from 8 bits. All data is represented by one or more bytes. Text typed into a word processing program is translated into numbers using an encoding scheme just as images or MP3 tracks or video clips are represented as a sequence of binary digits. Even the instructions that a microprocessor chip is given to execute and thus manipulate those word processing documents or songs or films are simply binary numbers.
Machine Instructions
Some randomly picked (and less than meaningful perhaps) Arduino ATmega machine instructions are
| Instruction | Machine binary instruction | Mnemonic |
| Add two number with carry | 0001 | adc |
| Logical AND | 0010 | and |
| Shift bits right | 1001 | asr |
A computer has something called a clock (sometimes built into the processor chip but otherwise to be found on the main processor board) that sends a regular sequence of pulses to the microprocessor chip with the Central Processing Unit (CPU) executing instructions in response. Many instructions are completed in a single cycle (the time between the start of one clock pulse and the following one) but some require multiple clock cycles to complete. Higher clock speeds result in more instructions being executed by a processor in a given unit of time although higher clock speeds generally consume more power.
In the earliest days of computing, computer programs consisted of just the binary machine instructions. As you might imagine, writing programs as a sequence of binary numbers was error prone and laborious even allowing for the expertise of the first generation of programmers who were most often key members of the computer development team. A certain David Wheeler at Cambridge University came up with the idea of using mnemonics for the machine instructions which could then be fed into a program called an assembler to generate the binary machine instructions. Writing programs using the mnemonics (and some of the other shortcuts introduced as part of the assembler capabilities) was much easier and allowed access to computing resources to be expanded beyond the immediate hardware development teams.
Even writing programs for a computer in an assembler language proved taxing for most. In response to this challenge, a number of “high level” programming languages were developed. These languages were usually “compiled” into assembly mnemonics before being finally translated to the machine binary codes ready for execution. While early higher level languages, at least, failed to bring computer programming to the masses, they did simplify the task of writing a program and thus freed the programmer to concentrate more on what needed to be done while being less bothered about the intricacies of how that should be managed by the processor.
As an example, an assembler fragment to add two small numbers together might look like the following (a register by the way is just a storage location within the CPU).
| Assembler statements | Meaning |
| lds r1,$FF00 | Load register 1 with the byte found at memory address FF00 (note a hexadecimal number) |
| lds r2,$FF10 | Similarly load register 2 with the byte found at address FF10 |
| add r1,r2 | Add the content of register 2 to register 1 |
| sts $FF00,r1 | Write the result in register 1 back to the address FF00 |
While in a higher level language, such as C, the same instructions might be written in a single line of code:
a = a + b;
Which means: add the two values the programmer gave the names a and b together and store the result as a.
The C language statement is just about equivalent to the assembler instructions but the programmer has not had to decide which arithmetic registers (computer resources) are currently not being used to hold something else and has not been required to keep track of the location in memory of each data item. In assembler, if the needed resources had not been available then additional code would have been required to juggle data and locations while this simple addition was executed. With a higher level language it is the compile process which does the heavy lifting by working out just what processor resources to use to execute a given program line.
Some programming languages such as Java, Visual Basic or C# are supported by a large “runtime system”. The runtime system manages program execution and provides services such as access to files on hard drives or connections to the Internet. The Microsoft .NET runtime, as an example, supports a range of programming languages across more than one operating system running on a range of computer chips.
The C programming language does not make use of a runtime system as it is designed to run “close to the metal” (as the expression has it). This makes C the ideal tool to write those operating systems themselves and of course is perfect for a microprocessor like the Arduino where we want to manipulate the processor directly for maximum efficiency in a minimalist environment.
Data Types
While all data manipulated by a computer is represented as a binary number it is generally useful for a programming language to keep track of just what sort of data (or type) each number represents.
Some programming languages are described as “typed“ (sometimes “strongly typed”) while others supporting something called “dynamic typing”. In typed languages, all data elements are assigned to a defined type – one might be a string of text characters while another might be an integer value. This allows the compiler to check the types of data elements used in an expression to ensure that they are appropriate – the division of text data by an integer for instance would probably be an error. Dynamic typing allows data to be transformed from one type to another, dynamically. However this can result in unexpected results. A JavaScript programming language example might be:
aNum = ‘5’; // assign the text character 5 to variable aNum
anotherNum = 4; // assign the integer 4 to anotherNum
newVal = aNum + anotherNum;
You can perhaps guess that JavaScript uses dynamic typing and the question is, should newVal contain the text characters ‘54’ or the number 9? JavaScript has a rule for deciding this but the key point is that it is often difficult to discern the programmer’s intention. The programmer might have wanted one result but maybe ended up with the other. Now if that went unnoticed and the result was fed into another process then the end result could be chaotic to say the least.
Where does C stand on the question of types? In practice, this is a good question to get a group of programmers started on a vigorous debate. We will just accept for the moment that C has defined types for all of the data elements in a program. Program expressions can be checked at compile time to catch type errors. However, C can be used to coerce one value type into another and C has no type checking during execution. This can lead to some spectacular errors but is also a strength. C gives you control and the power to do what you will – and leaves it to you, the programmer, to make sure your code delivers what you intend.
Information on negative binary integers is available here.